Chain Switching Rule

The chain switching rule in IOTA 2.0 is a tool that enables liveness for finalizationThe irreversible operation where blocks receive sufficient approval and consensus, ensuring their permanence. after an asynchronous period ends and allows for the safety property of the finalization flag. With the chain switching rule, a node finds the heaviest chain and syncs from that chain, i.e., updates the locally maintained Tangle and the ledger.

Cumulative Weight

Weight of a Slot Commitment

Let $(C_1,\ldots,C_s,C_{s+1},\dots,C_{s+d})$ be a slot commitment chainA chain created by a sequence of slot commitments. It is used to determine eligible blocks and finality.. Let $A$ denote the set of all accepted validation blocksValidation Blocks is a special type of blocks that are issued by members of the Validator Committee. These block allows to reach consensus in the network. that are committed into $C_{s+1},\dots,C_{s+d}$ such that each block from $A$ approves $C_s$. Then the weight of the slot commitment $C_s$ with drifting parameter $d$ (in the code, it is set to parameter maxCommittableSlotAge) is defined as the sum of voting weights of committee members who issued a block from $A$, i.e. those committee members who approve this commitment during $d$ slots after slot $s$, i.e.

$$W(C_{s})=\sum_{i\in IssuerIDs(A)}W_i(e),$$

where slot $s$ belongs to epochA specific time period during which a dedicated committee is responsible for driving consensus. Epoch consists of multiple slots. $e$.

Example

In this example, the committee consists of $7$ nodes. Their weights are specified at the bottom of the following image.

Suppose that the current slotTime interval of fixed duration. The protocol divides time into non-overlapping slots. For each slot, nodes generate a slot commitment which encapsulates all accepted blocks and transactions issued within this time interval. commitment chain consists of two elements $(C_1,C_2)$. The weight of the commitment $C_1$ with drifting parameter $d=3$ can be computed as follows:

All the blocks, that are included in the set $A$ in the above definition, are highlighted with a border. The weight $W(C_1)$ is equal to the sum of voting weights of the blue, orange, purple, grey, and green nodes, i.e. $W(C_1)=1+2+3+1+1=8$. The weight of the green node that commits to $C_2$ is counted as $C_2$ is an extension of $C_1$ and the corresponding block of the green node is issued at slot $4$, which is covered by the drifting parameter. The weight of the grey node is counted only once in $W(C_1)$ even though it has issued two blocks satisfying the requirements. The weight of the yellow node that commits to $C_1$ at slot $5$ is not counted as this slot is not covered by the drifting parameter $d=3$, i.e. $1+3<5$.

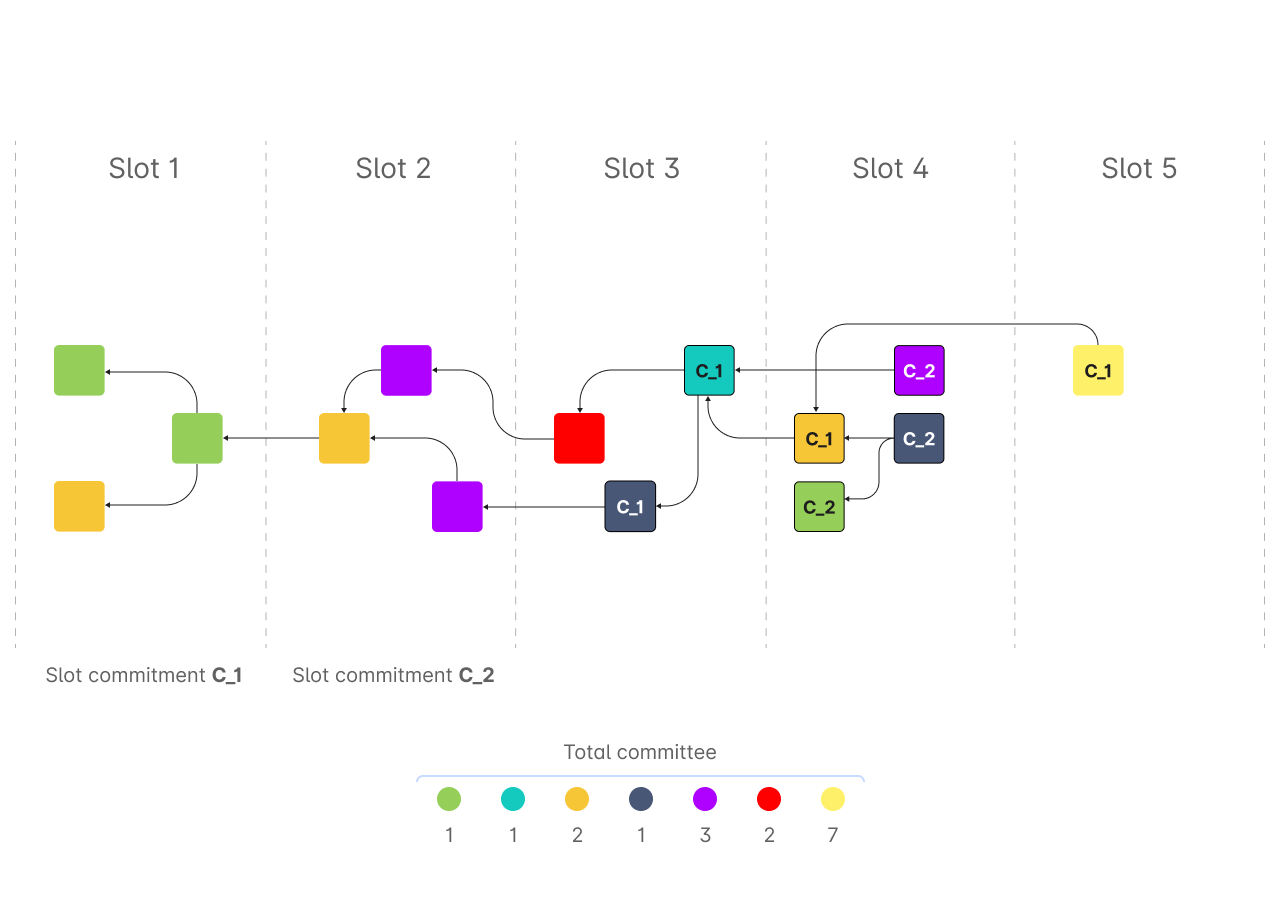
Image: Illustration for computing the weight of a slot commitment.

Cumulative Weight of a Slot Commitment Chain

Let $(C_1,\ldots,C_s,C_{s+1}\dots,C_{s+d})$ be a slot commitment chain. Then the cumulative weight of the chain $(C_1,\ldots,C_s)$ with a drifting parameter $d$ is defined as

$$CW(C_1,\ldots,C_s)=\sum_{j=1}^{s}W(C_j).$$

Chain Switching Rule Algorithm

The chain switching rule relies on the last finalized slot and the cumulative weight of slot commitment chains.

Conflicting Slot Commitments

Two slot commitment chains are called conflicting if none of them is a prefix of the other. A slot commitment $C$ is called conflicting to a slot commitment chain if this chain is conflicting with the slot commitment chain that ends at $C$.

Suppose a node adopts a slot commitment chain $ch_{loc}=(C_1,\dots,C_{s+d})$ and receives a block $b$ from a conflicting slot commitment chain $ch_{fork}=(B_1,\dots,B_{s+d})$. Then the node proceeds with the following steps:

1. Find the slot index $f$ of the forking point, i.e. $C_1=B_1,\dots,C_f=B_f$ and $C_{f+1}\neq B_{f+1}$.
2. Check if the last finalized slot of the chain $ch_{loc}$ is greater than $f$. If yes, ignore the block $b$ and stay on the chain $ch_{loc}$. Otherwise, proceed with the next step.
3. Check if the inequality holds $CW(B_1,\dots,B_s)\le CW(C_1,\dots,C_s)$. If yes, ignore the block $b$ and stay on the chain $ch_{loc}$. Otherwise, proceed with the next step.
4. If there exist at least optsChainSwitchingThreshold=3 consecutive indices when the cumulative weight of the conflicting chain $ch_{fork}$ is larger than the one of the currently adopted chain $ch_{loc}$, i.e. $CW(B_1,\dots,B_{t})>CW(C_1,\dots,C_{t}), CW(B_1,\dots,B_{t+1})>CW(C_1,\dots,C_{t+1}), CW(B_1,\dots,B_{t+2})>CW(C_1,\dots,C_{t+2})$ for $f\le t \le s-2$, then request the attestation for the cumulative weightA system for valuing transactions. The cumulative weight of a transaction increases with each additional transaction that references it. A path through transactions with a higher cumulative weight is preferred when selecting tips., validate the attestations and switch $ch_{loc}$ to $ch_{fork}$ after the current slot is completed.

Chain Switching

Switching the chain only happens when the current slot is finished. This property is important for the safety of the finalization flag as it does not allow honest nodes to vote on conflicting chains within one slot.